Tamarin is a tool for checking cryptographic security protocols (such as TLS or WireGuard). In this post, I try it out on some (very old, but simple) protocols from Applied Cryptography.

Table of Contents

• Introduction
• Key Exchange with Symmetric Cryptography
  • Checking it's usable
  • Checking it's secure
• Key Exchange with Public-Key Cryptography
• Interlock Protocol
• Key and Message Transmission
  • Fixing it
• Conclusions

Introduction

I recently came across Tamarin while reading about WireGuard, and decided to try it out. You give Tamarin a description of a security protocol and some properties you'd like to check, and for each one it tries to prove that it's true (or find a counter-example). It can normally do this automatically, but there's also a web UI that lets you direct the solver manually:

The Tamarin UI

This interested me because I don't feel that I have a good understanding of what makes a cryptographic protocol secure, and I thought making formal models might help. The Tamarin site has a tutorial and a free (draft) book, but you should be able to follow this blog post without having read them.

Applied Cryptography was a popular (but now long-obsolete) book showing "how programmers and electronic communications professionals can use cryptography". I have the second edition, from 1996. Testing Tamarin on very old protocols has several advantages:

1. Old protocols tend to be much simpler than newer ones.
2. It's more likely I'll be able to find some weakness.
3. If I do find a problem, it doesn't need reporting anywhere.

Chapter 1 of the book introduces some basic concepts. Chapter 2 introduces the idea of protocols and the conventional names used (Alice wants to use the protocol to talk to Bob; Trent is a trusted third party; Mallory is an attacker, intercepting, modifying and replaying messages). Chapter 3 starts going though some useful protocols, so I started there...

Key Exchange with Symmetric Cryptography

Chapter 3 ("Basic Protocols") starts with a key exchange protocol in which Alice and Bob communicate using a session key that they get from Trent, a trusted third party. Alice and Bob have each previously agreed long-term keys to communicate with Trent:

1. Alice calls Trent and requests a session key to communicate with Bob.
2. Trent generates a random session key. He encrypts two copies of it: one in Alice's key and the other in Bob's key. Trent sends both copies to Alice.
3. Alice decrypts her copy of the session key.
4. Alice sends Bob his copy of the session key.
5. Bob decrypts his copy of the session key.
6. Both Alice and Bob use this session key to communicate securely.

A Tamarin file has this basic structure:

theory Example1
begin

builtins: symmetric-encryption

...

end

symmetric-encryption gets us a function senc(msg, key) to represent msg encrypted with key, plus an equation allowing the attacker to recover msg if they have key.

Tamarin represents the state of the world as a collection of state facts. You can use whatever fact names you want, but there are a few special built-in ones:

• Fr(x) indicates that x is a fresh unguessable value that isn't known to anyone yet. There is an endless supply of such facts, as you can always generate a new random number.
• Out(msg) says that msg was sent to the network (which is controlled by the adversary).
• In(msg) says that msg was sent from the network/adversary.

The behaviour of the system is given by a set of rules, each of which can consume state facts and produce new ones.

The first rule allows people to register with the trusted authority Trent:

rule Register:
    [ Fr(k) ]
  -->
    [ !Key($A, 'Trent', k) ]

This rule consumes a fresh unguessable value k and produces a fact that some public name $A has registered that key. Variables starting with $ are restricted to public (guessable) values. The adversary knows all public values without having to see them first.

I'm using the state fact !Key('Alice', 'Trent', k) to mean that Alice has registered symmetric key k with Trent. The secord argument of !Key is always 'Trent'; I just included it for clarity. !Key starts with ! to indicate that this is a persistent fact - it can be used multiple times without being consumed.

The Tamarin book says we also need a rule to represent someone revealing their registered key:

rule Reveal_key:
    [ !Key($A, 'Trent', k) ]
  --[ Reveal($A) ]->
    [ Out(k) ]

This says that if $A is using key k then they might send it out on the network (Out), which has the effect of handing it to the adversary. The --> arrow here is annotated with an action fact Reveal($A). These facts are like log messages, and are used when checking properties. They allow us to say things like "Assuming Alice doesn't reveal her key, ...".

There are two reasons to include this rule. First, we could model what happens if e.g. Alice reveals her key and Bob doesn't. Second, and more important, this allows the attacker to get hold of registered keys. Without this, we ignore the possibility of Mallory having access to any keys at all.

I didn't model the possibility of Trent revealing any keys, as that's obviously fatal.

Then I wrote four rules describing the protocol. $A (e.g. Alice) sends a message to Trent saying she wants to talk to $B (e.g. Bob):

rule A1:
    [ ]
  -->
    [ Out(<$A, $B>),
      A1_sent($A, $B) ]

She also adds an A1_sent fact to remember that she requested this. The convention is that the first argument of a fact is the actor owning it, when that makes sense.

Note: the Out fact doesn't say where the message is going. That would be pointless, since the network isn't trusted and Mallory can route messages anywhere.

Trent receives the request, gets the registered keys for $A and $B, and generates a fresh session key for them (kab):

rule T:
    [ In(<$A, $B>),
      !Key($A, 'Trent', kat),
      !Key($B, 'Trent', kbt),
      Fr(kab) ]
  --[ Secret(kab), Honest($A), Honest($B) ]->
    [ Out( <senc(kab, kat), senc(kab, kbt)> ) ]

Trent replies with kab encrypted for each of them.

There are some more action facts here: Secret(kab) means that kab is supposed to be secret (not known to the adversary), assuming all the Honest parties don't reveal their registered keys. The names Secret and Honest aren't special, but they are suggested by the Tamarin book. We'll write properties using them later.

$A gets the two replies, decrypting the first using her key kat. She outputs mb (the encrypted message for $B, which she can't decrypt) and her message (msg) encrypted with the new session key:

rule A2:
    [ A1_sent($A, $B),
      !Key($A, 'Trent', kat),
      In(<senc(kab, kat), mb>),
      Fr(msg) ]
  --[ Sent($A, $B, msg),
      Secret(msg), Honest($A), Honest($B) ]->
    [ Out( <mb, senc(msg, kab)> ) ]

Action facts indicate that msg is supposed to be secret, and that $A sent msg to $B, as that's something we'll want to check.

Finally, $B uses his registered key kbt to decrypt the session key kab, and uses that to decrypt the message, recording the fact that he got it:

rule B:
    [ !Key($B, 'Trent', kbt),
      In( <senc(kab, kbt), senc(msg, kab)> ) ]
  --[ Received($B, $A, msg) ]->
    [ ]

Checking it's usable

The book recommends checking that the protocol works in at least one case, which can be done like this:

lemma works:
  exists-trace
    "Ex msg #i #j.
      Sent('Alice', 'Bob', msg)@i
      & Received('Bob', 'Alice', msg)@j"

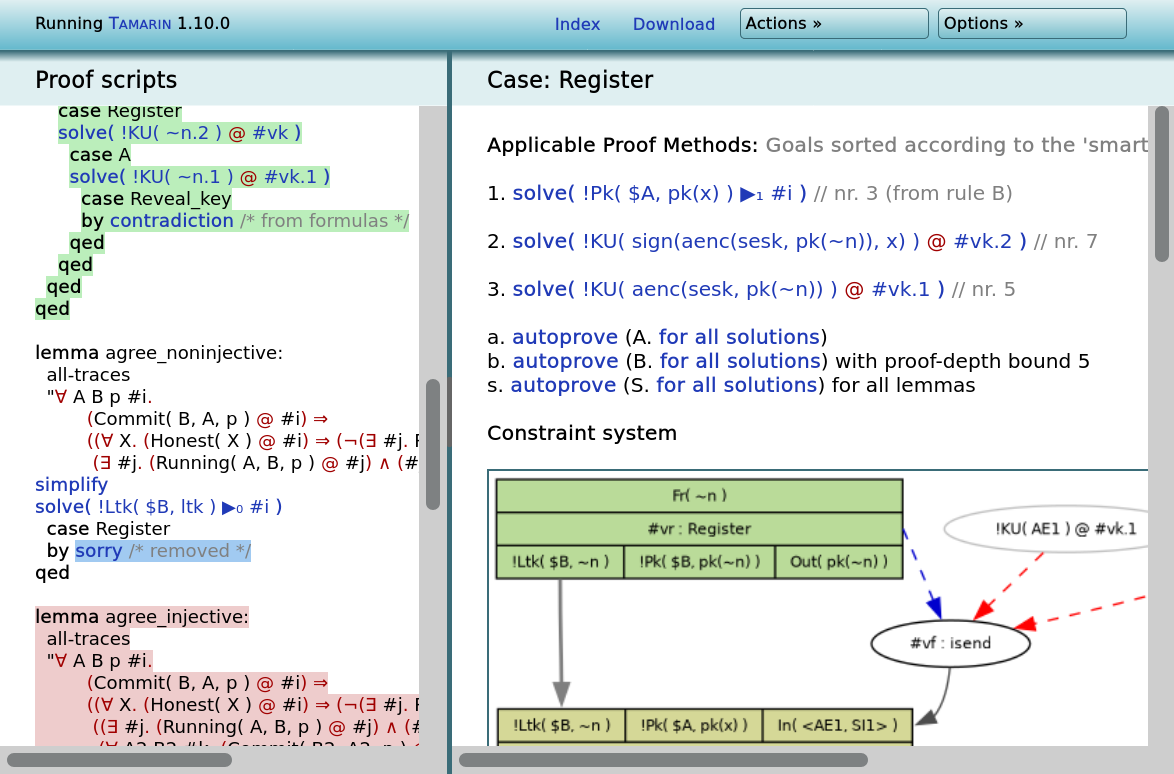
This says that there exists some trace (possible sequence of action facts) in which there exists a message msg and time-points #i and #j, such that Alice sent msg to Bob at time i and Bob received it at time j. Tamarin finds this example of it working:

An example trace

The boxes represent the rules being used. For example, the top two Register boxes show Alice and Bob registering their keys. Ellipses represent actions of the adversary/network. They are also generated by rules, but are shown differently by default.

The example isn't quite what I initially expected. Here's what happened (from top to bottom):

1. Alice and Bob registered their keys.
2. Mallory asked Trent to generate a session key for Alice to talk to Bob.
3. Trent generated a session key and sent out the two encrypted copies.
4. Mallory removed the encrypted message for Bob and replaced it with an arbitrary message before forwarding to Alice.
5. Alice sent a request to Trent asking for a session key with Bob, which got discarded.
6. Alice received the session key from Trent, along with Mallory's arbitrary message. She forwarded Mallory's part, adding her message (encrypted with the session key).
7. Mallory replaced the arbitrary message with the original message to Bob from Trent.
8. Bob received and decrypted the message.

This is a bit more general than the expected path:

• Trent can receive the request for the key before Alice sends it, as there's nothing to stop Mallory sending requests.
• Alice forwarding Trent's message to Bob is irrelevant for modelling purposes. Mallory controls the network and anything can be sent anywhere.

There doesn't seem to be a built-in way to ask for an example where Mallory just forwards messages. However, you can replace In and Out with something else (e.g. Secure_net) to model a network without an attacker:

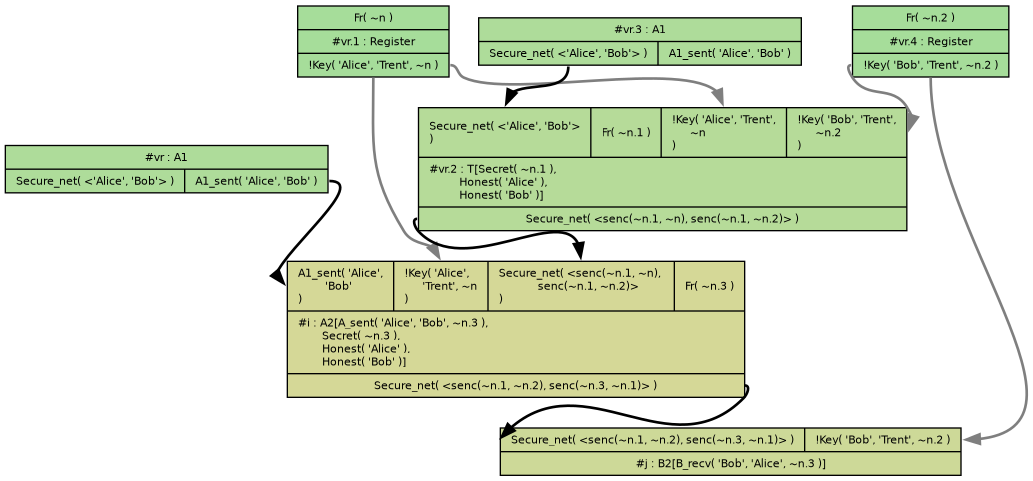A protocol example without Mallory

Checking it's secure

Next, I ask Tamarin to check that no secrets are leaked, using a standard pattern recommended by the Tamarin book.

For all secrets k (marked Secret(k) at time #i), if all actors A required at #i to be honest never reveal their keys, then there is no time #j at which Mallory knows k (K(x) means the adversary knows x):

lemma secrets:
  "All k #i. Secret(k)@i ==>
     (All A. Honest(A)@i ==> not Ex #j. Reveal(A)@j)
     ==> (not Ex #j. K(k)@j)"

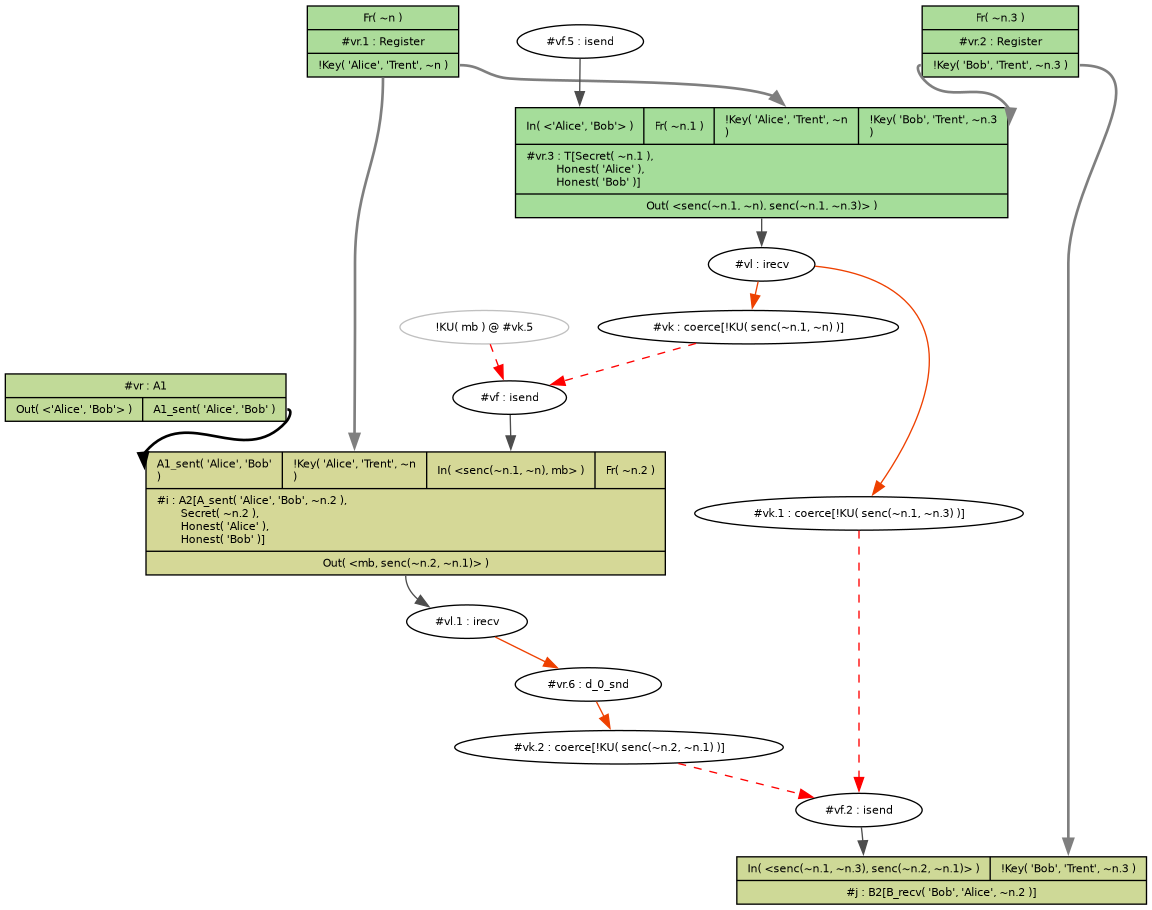
Tamarin immediately shows a counter-example:

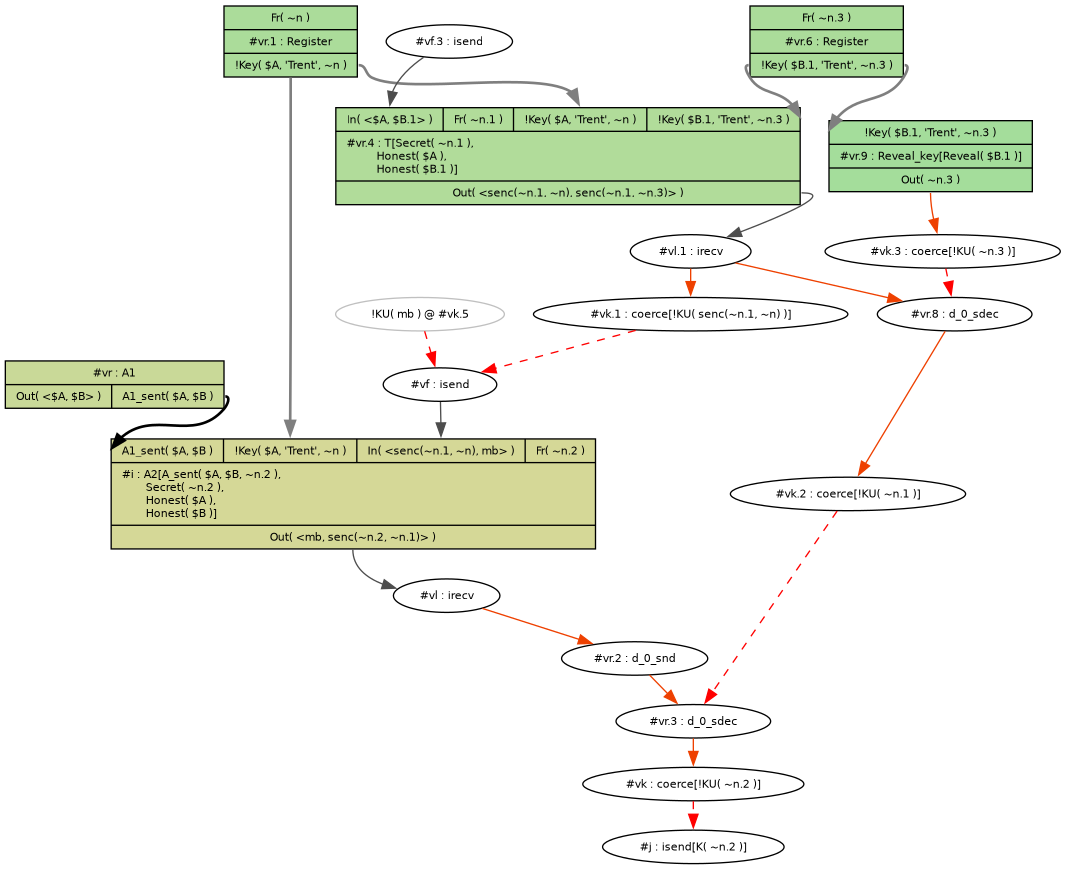Mallory reads the secret message

Here's what happened:

1. Alice ($A) and Mallory ($B.1) register keys with Trent.
2. Mallory asks Trent for a session key between Alice and himself.
3. Alice asks Trent for a session key between herself and Bob.
4. Mallory sends the reply to his request to Alice.
5. Alice encrypts her message to Bob with the Alice-Mallory session key and sends it.
6. Mallory decrypts it.

I'm not surprised this protocol doesn't work. The Tamarin book starts with a more complicated version of it, where Trent says who each key is for, and shows that it still has problems.

I find it odd that Applied Cryptography doesn't warn about this when describing the protocol. It does mention various improvements to it later in the chapter, so the flaws are obviously known. The introduction says the book intends to be "both a lively introduction to the field of cryptography and a comprehensive reference". For a reference aimed at programmers, I'd expect to see warnings on protocols with known problems. The book does warn that this protocol relies completely on Trent though, and is perhaps just here to contrast with the next example, using public-key cryptography.

Key Exchange with Public-Key Cryptography

With separate public and private keys, the next protocol is much simpler:

1. Alice gets Bob's public key from the KDC [Key Distribution Centre].
2. Alice generates a random session key, encrypts it using Bob's public key, and sends it to Bob.
3. Bob then decrypts Alice's message using his private key.
4. Both of them encrypt their communications using the same session key.

The Tamarin book recommends modelling a PKI (Public Key Infrastructure) like this:

builtins: asymmetric-encryption

rule Register:
    [ Fr(ltk) ]
  -->
    [ !Ltk($A, ltk), !Pk($A, pk(ltk)), Out(pk(ltk)) ]

rule Reveal_key:
    [ !Ltk($A, ltk) ]
  --[ Reveal($A) ]->
    [ Out(ltk) ]

Here, we have !Ltk for the long-term (private) key and !Pk for the public one. pk(x) represents the public key corresponding to private key x. Register immediately leaks the public key to the adversary, as we want to prove the protocol works assuming that public keys are known.

The behaviours are simpler than before:

rule A:
    [ !Pk($B, pkB),
      Fr(sesk) ]
  --[ Running($A, $B, <'R', 'I', sesk>),
      Secret(sesk), Honest($B) ]->
    [ Out(aenc(sesk, pkB)) ]

rule B:
    [ !Ltk($B, ltk),
      In(aenc(sesk, pk(ltk))) ]
  --[ Commit($B, $A, <'R', 'I', sesk>) ]->
    [ ]

The Running and Commit action facts here are suggested by the Tamarin book:

• Commit(B, A, p) means that B believes he has agreed parameters p with A.
• Running(A, B, p) means that A is trying to agree p with B.
• <'R', 'I', sesk> means that the committing party is the Responder and the other is the Initiator. The roles are ordered to match the Commit fact in both cases.

Here's an example of it working:

lemma works:
  exists-trace
    "Ex p #i #j.
      Running('Alice', 'Bob', p)@i
      & Commit('Bob', 'Alice', p)@j"

Using asymmetric encryption

The secrets lemma from before passes (and only Bob needs to be honest).

The Tamarin book also recommends checking agreement, which I did like this:

lemma agree_injective:
  "All A B p #i.
     Commit(B, A, p)@i ==>
       (All X. Honest(X)@i ==> not Ex #j. Reveal(X)@j) ==>
         (Ex #j. Running(A, B, p)@j & j < i)
         & (All A2 B2 #k. Commit(B2, A2, p)@k ==> #i = #k)"

This says that if B thinks he has agreed p with A, and all parties required to be honest are, then:

• A was trying to agree p with B in the past, and
• this is the only Commit with p.

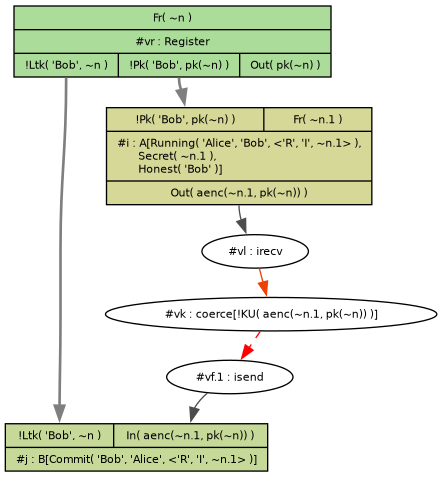
Tamarin finds an obvious flaw with this protocol:

Mallory tricks Bob

Here:

1. Mallory ($A.1) generates a session key and encrypts it for Bob.
2. Bob decrypts the key and believes he is talking to Alice.

Not very surprising; Alice doesn't use her private key for anything in this protocol! Is Applied Cryptography only considering passive eavesdroppers? But the next section ("Man-in-the-Middle Attack") does consider active attacks when sharing the public keys (which I didn't model here), so this does seem to be in-scope.

This flaw would be pretty obvious if you were writing a service with multiple clients, because how do you know which client it is? But you might conceivably miss it if there were only one client.

Interlock Protocol

The next section presents the Interlock Protocol. This is designed to stop man-in-the-middle attacks. The idea is that Alice sends half of her message first (e.g. every other bit), so the Mallory can't decrypt it yet even if he tricked Alice into using his public key. Then Alice expects the first half of Bob's response before she sends the rest of her message.

This makes no sense to me. How can Bob commit to his response before being able to decrypt Alice's request? I read the Interlock Protocol's Wikipedia page, and that seems to suggest that Alice and Bob also require pre-shared passwords. But then why not pre-share their public keys and solve the problem more simply? Also, Wikipedia points out a simple attack on it. I'm going to skip this one.

Key and Message Transmission

In this section, the book finally offers a solution to active attackers. Curiously, it's not the main topic, which is that Alice can send her message (M) without waiting for Bob:

1. Alice generates a random session key, K, and encrypts M using K.
2. Alice gets Bob's public key from the database.
3. Alice encrypts K with Bob's public key.
4. Alice sends both the encrypted message and encrypted session key to Bob.
   For added security against man-in-the-middle attacks, Alice can sign the transmission.
5. Bob decrypts Alice's session key K, using his private key.
6. Bob decrypts Alice's message using the session key.

Modifying the previous example to model this was easy enough, but including the message M clutters things up a bit, so for simplicity I removed it for the blog post:

builtins: asymmetric-encryption, signing

rule A:
  let c = aenc(sesk, pkB) in
    [ !Ltk($A, ltk),
      !Pk($B, pkB),
      Fr(sesk) ]
  --[ Running($A, $B, <'R', 'I', sesk>),
      Secret(sesk), Honest($B) ]->
    [ Out( <c, sign(c, ltk)> ) ]

rule B:
  let c = aenc(sesk, pk(ltk)) in 
    [ !Ltk($B, ltk),
      !Pk($A, pkA),
      In( <c, sig> ) ]
  --[ _restrict( verify(sig, c, pkA) = true ), Unique(<$B, sig>),
      Honest($A), Honest($B),
      Commit($B, $A, <'R', 'I', sesk>) ]->
    [ ]

restriction r_unique:
  "All m #i. Unique(m)@i ==>
     All #j. Unique(m)@j ==> #i = #j"

• sign(c, ltk) is Alice's signature of the ciphertext c with her long-term private key.
• _restrict( verify(sig, c, pkA) = true ) says rule B can only be used if the signature matches.
• Unique(<$B, sig>) says Bob will reject signatures he has seen before, to prevent replay attacks.

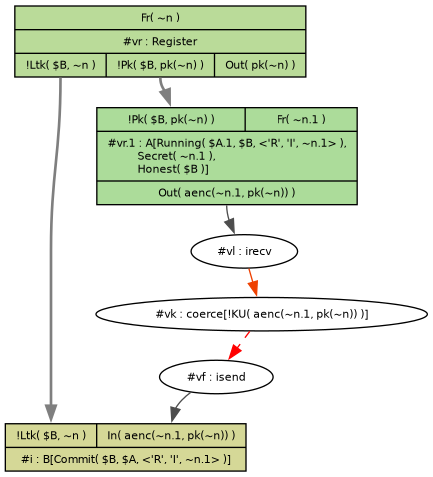
Tamarin immediately finds a counter-example:

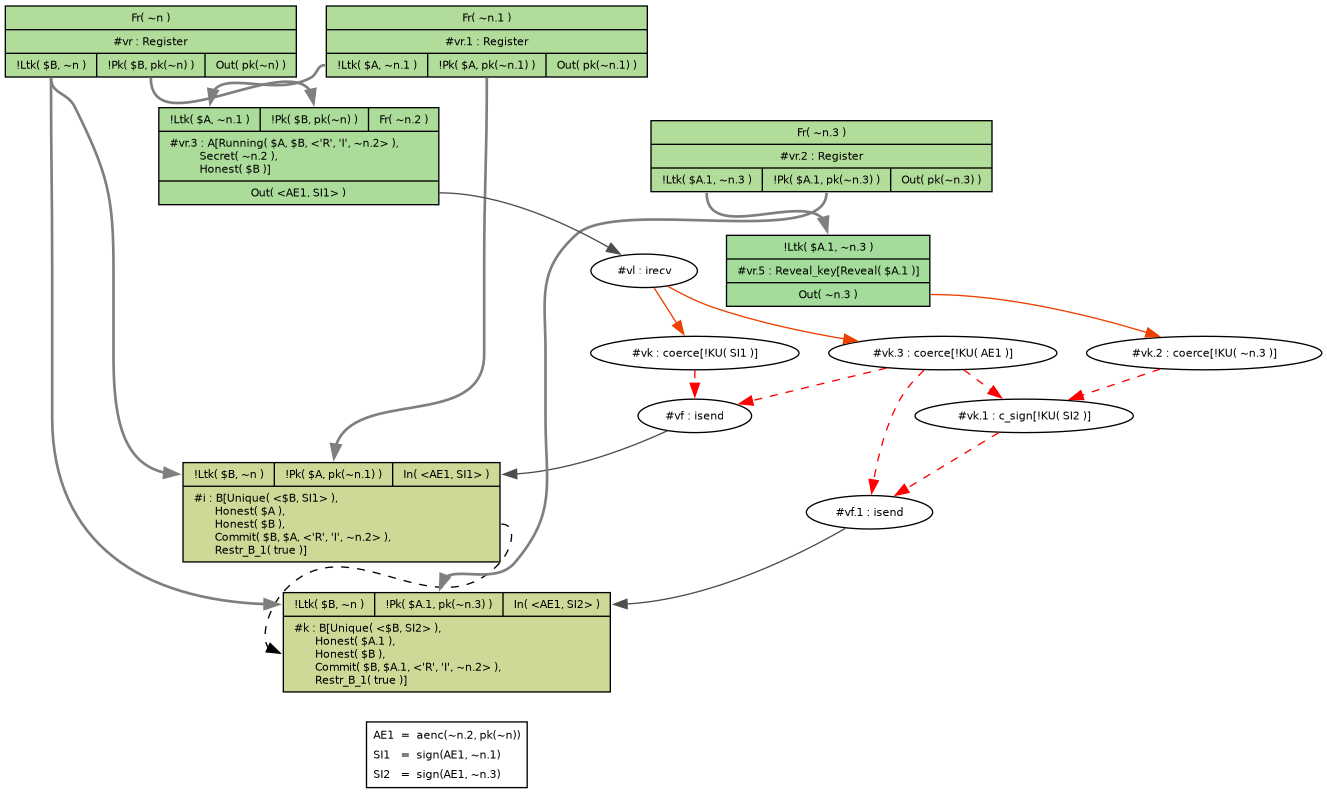Doesn't work with even with signing

Here's what happened:

1. Alice ($A), Bob ($B) and Mallory ($A.1) register public keys with the PKI.
2. Alice generates a new session key (~n.2), encrypts it for Bob, and signs the ciphertext with her public key.
3. Mallory removes Alice's signature and re-signs with his key (c_sign).
4. Bob commits to using ~n.2 to talk to Mallory, but is actually talking to Alice.

This could be a problem if, say, Bob is a file-sync service and Alice is trying to send her files. The result would be Alice's files getting stored in Mallory's account at Bob rather than her own.

This seems like a more interesting attack than the previous ones; a non-cryptographer like me could easily miss this.

However, I think it's also a bit of a fluke that Tamarin detected it. The error is detected because Bob also gets Alice's original message, and now has two conflicting Commits. But to make agree_injective pass you need to prevent simple replay attacks (where Malloy just sends Alice's message twice). I did that using Unique(<$B, sig>) to ignore duplicate signatures, but I could instead have used Unique(<$B, sesk>) to ignore duplicate session keys. In that case, Tamarin wouldn't spot the problem.

I think the real issue here is that I'm only checking things from Bob's point of view. In the Tamarin book, it generally also has a Commit on Alice to check that if Alice thinks she's talking to Bob, then Bob thinks he's talking to Alice. Checking just Bob's Commit isn't enough; he thinks he's talking to Mallory and Mallory isn't Honest so we don't care. But in this protocol Alice commits to Bob without exchanging any previous message, so this Running/Commit system won't do.

Fixing it

If I add Alice's name to the encrypted session key (e.g. let c = aenc(<$A, sesk>, pkB)) then Tamarin reports everything is fine. Is this actually safe, though? Tamarin assumes that the only thing Mallory can do with an encrypted message is decrypt it (given the key). But what about if he modifies the ciphertext?

Applied Cryptography has previously introduced us to the one-time pad encryption scheme. If Alice encrypts "Alice,1234" with a one-time pad and signs it as from "Alice", then Mallory knows the first 5 characters are "Alice" and can recover the first 5 characters of the pad, then replace the name with any other 5-character name he has registered without disturbing the key.

I suppose better encryption schemes prevent that sort of thing, but I'm not sure. My fix relies on encryption (rather than signatures) to prevent tampering, which seems risky.

Chapter 16 of the Tamarin book ("Advanced modeling of cryptographic primitives") notes that Taramin's default models of digital signatures and hashes make assumptions that are not true for many real-world algorithms. It has little to say about encryption though, except this:

Real-world symmetric encryption schemes, such as AES, protect against an adversary trying to learn the message that was encrypted. However, they do not provide authentication: if we provide a random string to the AES decryption algorithm instead of a real ciphertext, it will not fail, but instead produce a (random looking) output.

Thinking on about this, I wonder if I've misinterpreted the protocol. The text in Applied Cryptography is:

For added security against man-in-the-middle attacks, Alice can sign the transmission.

( I dislike the word "added" here. It would be more reassuring without it. Is it just saying that signing helps a bit, but not completely? )

I assumed that "the transmission" meant the ciphertext, but I don't think "transmission" has been formally defined. Could "the transmission" mean "the plaintext"? Though if so, there are two things that could be signed here (the session key and the message), and it doesn't say which one it means.

OK, reading around a bit further, I see that Chapter 2 says "signing before encrypting is a prudent practice", so I guess that's what it meant (looks like this is still being debated today, e.g. on crypto.stackexchange.com). If so, this still seems like a good reason to use Tamarin - checking that you haven't misunderstood the protocol!

Hmm, but Tamarin says it still doesn't work if Alice signs the session key first, then encrypts:

1. Alice generates a session key to talk with Mallory, signs it, and encrypts it for Mallory.
2. Mallory decrypts the signed key and re-encrypts it for Bob.
3. Bob thinks he's talking to Alice, but he's really talking to Mallory.

Well then I have no idea what the book meant.

Conclusions

I found Tamarin fairly easy to use, though a few things caused me a bit of trouble:

• I forgot the ! in !Key at first, so the fact could only be used once. Then Tamarin couldn't find an example of it working and it took me quite a while to realise why.

• If you forget a close quote in a lemma body, it reports a confusing syntax error.

• Using a function without declaring it (e.g. pk(x)) is reported as a confusing syntax error.

As well as using $ for public values, the book also uses ~ for "fresh" ones. However, it also says that doing that can affect the traces (see "Effects of type annotations" in the book) so I avoided using it myself. I'm not sure why it would be needed.

Tamarin's solver can usually solve lemmas in a second or so by itself. Sometimes though it gets stuck in a loop. This happened with my Secure_net example in this post. When that happens, you can either direct the solver manually using the UI (which is mostly useful for discovering what the problem is), give hints to tell it to try exploring other branches first, or write a helper lemma (tagged with [reuse]).

One important thing to be aware of is that Taramin files can execute external commands, so never ask Tamarin to verify a protocol without reading it first (this feature is mentioned on page 253 of the book, under "Oracles").

The main problem I have with Tamarin is that the built-in models of e.g. encryption seem a bit unrealistic, and so I'm not sure how much I trust a verified proof to be secure with a real algorithm rather than the idealised one, as it seems hard to know what assumptions it's making.

Whereas after Using TLA+ to Understand Xen Vchan I feel confident that the (fixed) protocol actually works, the situation seems different with cryptography. I still wouldn't feel confident that I'd designed a secure protocol, even if Tamarin verified it.

Making models of the protocols in Applied Cryptography was a useful way to understand them better. Trying to formalise them certainly made me realise how vague the book is! The book often didn't indicate what properties you could expect the protocols to provide (e.g. whether a protocol was secure with an active attacker), or mention problems that would be addressed later in the book!

I suppose things were different when the book was published in 1996. SSL and SSH had only just arrived in 1995 (with OpenSSH in 1999), and most things still used plain text then; Internet security relied on people being too polite to peek at other people's traffic.

As well as finding flaws in protocols, and discovering what properties protocols provide, Tamarin also seems useful to check that you've understood the description of a protocol. Including a Tamarin model when describing a protocol would avoid a lot of confusion.